PID制御は、以下の式で実現されるフィードバックコントローラです。
C(s)=KP(1+1/TI*1/s+TD*s)
すなわち、コントローラへの入力信号の比例・積分・微分要素を足し算した値を出力します。 このとき、各要素の重みになるのが、KP：比例ゲイン、TI：積分時間、TD：微分時間です。 比例は現在、積分は過去、微分は未来を意味し、これらのKP、TI、TDのPIDパラメータを うまく調整することで、所望の制御性能を実現します。
もう少し詳しく説明すると、比例要素はゲイン補償を、積分要素は位相遅れ補償を、 そして微分要素は位相進み要素を実現しており、それぞれに大きな役目があります。 例えば、P（比例）制御だけで制御誤差を減少させようとした場合、KPを大きく設定する必要が ありますが、ある一定のところから誤差が減少しなくなります。 このとき残った制御誤差を定常位置偏差と呼びますが、これをゼロにするための働きを持つのが I（積分）になるというわけです。 積分要素を入れることによって、過去の誤差情報を取り入れることができるので、 定常偏差をゼロにすることができます。 ただし、設定値が一定かステップ関数の場合にはゼロに出来ますが、ランプ応答などの場合にはゼロにする ことができず、このとき残る誤差を定常速度偏差と呼びます。 レベル制御や圧力制御などの場合には、ランプ設定値にもうまく追従することができます。 これは制御系（一巡伝達関数）の持つ、積分器（原点極）の数によって判別することができます。
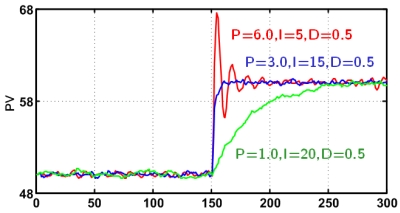
さて、次にD（微分）動作を入れることによって、誤差の未来値（傾き）を知ることができるので、 即応性と向上させたりオーバーシュートを防ぐことができます。 しかしながら、P・I・Dともにうまく設定しないと設定値変更の際に不足減衰や振動を発生するので プロセスの特性に合わせた値を適切に設定する必要があります。

また、定値制御の際にも一見うまく制御できているように見えても、外乱が入ったときなどに うまくその影響を抑えられない場合があります。 これもPIDパラメータの調整に問題があることが多く、適切に調整できれば外乱後のハンチングを 発生することもなく、外乱を抑圧することが可能な場合があります。
PIDパラメータの調整法には古くから様々な方法が提案されていますが、 中々実用面において手数を要したり、理想的な信号が採取できないがためにうまくいかないことが 多いのが現実です。 ADAPTEXでは、このような問題に対して制御性能評価ベースのPID調整技術を有しており、 今までにない効率性と最適性でPIDパラメータの計算を可能にしています。